(G. Tomasi di Lampedusa, Il Gattopardo)
- posta@leonardobandini.it
- skype: leobandini
NOVITA' SITO WEB: Nuova sezione aperta per i webinar, video lezioni di ingegneria e sismica. Disponibili le registrazioni di webinar dedicati all'ingegneria, alla sismica, alle principali analisi lineari e non lineari. Webinar disponibili in streaming on demand
E' possibile richiedere il file di matlab con l'integratore dell'equazione di moto per il calcolo di uno spettro di risposta elastico via mail, oppure mediante la sezione "Contatta" presente nel sito.
Risposta di un
oscillatore elastico ad un grado di libertà (Dynamic
responce of Single degree of freedom)
VERRÀ RISOLTA L'EQUAZIONE DIFFERENZIALE CHE RAPPRESENTA IL MOTO DI UN SISTEMA 1 D.O.F. OVVERO OSCILLATORE AD 1 GRADO DO LIBERTA' (1 DEGREE OF FREEDOM).
INIZIAMO CON LA DESCRIZIONE DEL MODELLO FISICO E LA DESCRIZIONE DELLA DINAMICA DI UN CORPO AD GRADO DI LIBERTA'[1 D.O.F. OVVERO OSCILLATORE AD 1 GRADO DO LIBERTA' - ONE DEGREE OF FREEDOM]
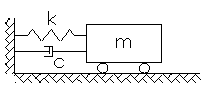
Massa M, rigidezza elastica K e smorzamento C.
L'EQUAZIONE DI MOTO DI QUESTO SISTEMA SOGGETTO A UNA FORZANTE ESTERNA F(t):
![]()
NEL CASO IN ESAME LA FORZANTE SISMICA E' DI NATURA INERZIALE, OVVERO VIENE PRODOTTA PER INERZIA INDUCENDO UN MOTO NEL TERRENO (SISMA).
![]() (1)
(1)
DIVIDENDO PER LA MASSA m SI PUO' RISCRIVERE L'EQUAZIONE COME:
![]()
DOVE:
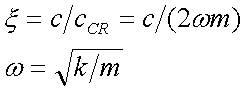 (2)
(2)
SE ANALIZZIAMO LA RISPOSTA DEL NOSTRO OSCILLATORE IMMAGINATO ABBANDONATO LIBERAMENTE DA UNA POSIZIONE DI NON EQUILIBRIO (u=u0) OTTENIAMO UNA OSCILLAZIONE CON PERIODO COSTANTE, MA CON AMPIEZZA DECRESCENTE NEL TEMPO. QUESTA RIDUZIONE DELL'AMPIEZZA E' PRODOTTA DALLO SMORZAMENTO.
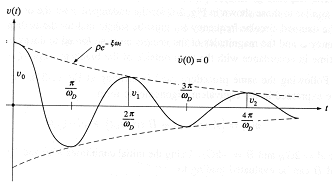
A QUESTO PUNTO IMMAGINIAMO DI AUMENTARE LO SMORZAMENTO, ARRIVEREMO AD UN CERTO VALORE PER IL QUALE, LO STESSO OSCILLATORE ABBANDONATO DA UNA POSIZIONE NON DI EQUILIBRIO TORNEREBBE VERSO L'ORIGINE MA SENZA OSCILLARE. QUESTO VALORE DI SMORZAMENTO E' CHIAMATO VALORE CRITICO ED E' INDICATO CON Ccr.
DEFINIZIONE DI SPETTRO IN TERMINI DI ACCELERAZIONI:
LO SPETTRO RAPPRESENTA LA CURVA INTERPOLANTE I VALORI DI RISPOSTA (IN TERMINI DI ACCELERAZIONE, VELOCITA' O DI SPOSTAMENTO) MASSIMI DI UN SISTEMA AD 1 GRADO DI LIBERTA' IN FUNZIONE DEL PERIODO FONDAMENTALE DEL SISTEMA STESSO.
IN ALTRE PAROLE IMMAGINIAMO DI AVERE UN SISTEMA AD UN GRADO DI LIBERTA', NEL QUALE POSSIAMO FAR VARIARE LA RIGIDEZZA. SU QUESTO SISTEMA RISOLVIAMO PER INTEGRAZIONE L'EQUAZIONE DI MOTO (1), OTTENENDO LA RISPOSTA DEL SISTEMA SOTTOPOSTO AD UNA STORIA DI ACCELERAZIONI. DELLA RISPOSTA VIENE PRESO IL VALORE MASSIMO PER OGNI STATO DI RIGIDEZZA DEL SISTEMA.
RICORDANDO (2) PARLARE DI RIGIDEZZA DI SISTEMA VUOL DIRE PARLARE IN ALTRE PAROLE DI PERIODO FONDAMENTALE:
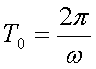
LO SPETTRO IN TERMINI DI ACCELERAZIONE E' QUINDI LA CURVA CHE INVILUPPA I MASSIMI DI RISPOSTA, SEMPRE IN TERMINI DI ACCELERAZIONI, IN FUNZIONE DEL PERIODO FONDAMENTALE DEL NOSTRO SISTEMA.
PER RISOLVERE CON MATLAB QUESTO PROBLEMA OCCORRE INNANZI TUTTO RICORRERE A SIMULINK PER GENERARE UN SISTEMA DI INTEGRAZIONE DELLA EQUAZIONE DIFFERENZIALE (1).
LO SCHEMA GENERATO IN SIMULINK E' IL SEGUENTE:
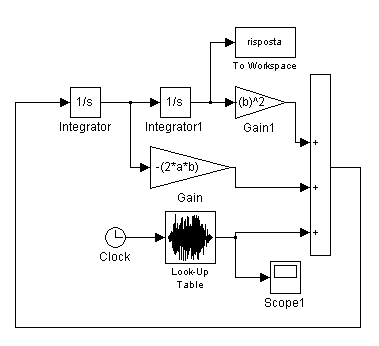
INSERENDO QUESTO OGGETTO DI SIMULINK LO POSSIAMO UTILIZZARE IN RUNTIME DA UNO SCRIPT DI MATLAB NEL SEGUENTE MODO:
clear
%a=0.05;
pi=3.14;
g=9.81;
a=input('inserire
il rapporto C/Ccrit [0.05]: ');
c=input('inserire
la Time History da analizzare [1..5] [0 per effettuare
la media]:
');
switch
c
case
0
mediaspettro;
break
case
1
load
ni1w;
T_c=ni1w(:,1);
m=ni1w(:,2)*g;
case
2
load
ni2w;
T_c=ni2w(:,1);
m=ni2w(:,2)*g;
case
3
load
ni3w;
T_c=ni3w(:,1);
m=ni3w(:,2)*g;
case
4
load
ni4w;
T_c=ni4w(:,1);
m=ni4w(:,2)*g;
case
5
load
ni5w;
T_c=ni5w(:,1);
m=ni5w(:,2)*g;
otherwise
fprintf('errore
nella scelta \n');
break
end
fprintf('Calcolo
spettro di risposta elastico in corso... \n');
for
I=1:100
T(I)=0.01*I;
end
for
J=1:40
T(I+J)=0.1*J+T(I);
end
for
I=1:140,
b=(2*pi/T(I));
sim spettro_sim
%load leo
X(I)=max(abs(risposta));
S(I)= 4*pi^2*X(I)/(T(I)^2);
end
fprintf('Calcolo
spettro di risposta elastico completato. \n');
load
spettroEC_B
TEC=spettroEC_B(:,1);
SEC=spettroEC_B(:,2);
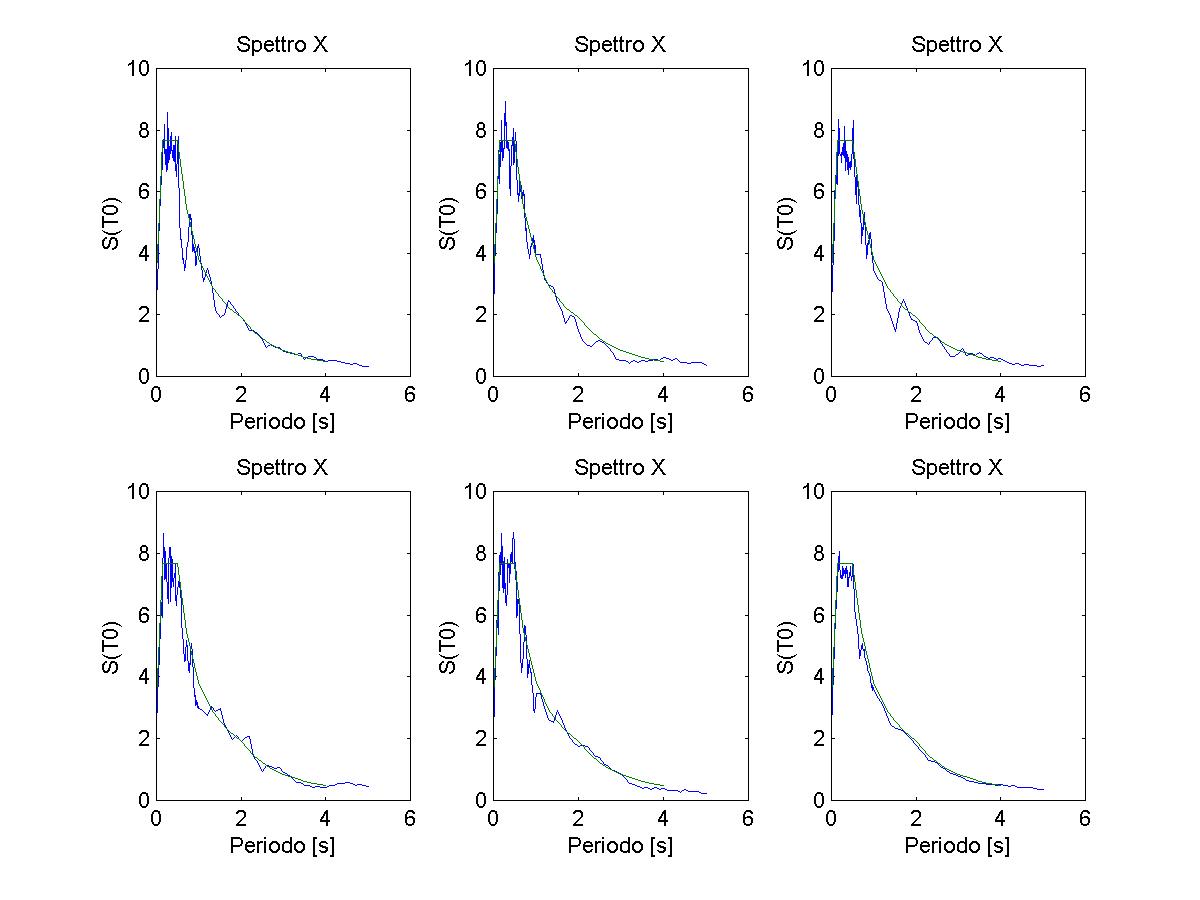
figure(1),plot(T,S,TEC,SEC),TITLE('Spettro X'),xlabel('Periodo [s]'),ylabel('S(T0)')
IN QUESTO CASO E' POSSIBILE TRACCIARE LO SPETTRO DI RISPOSTA ELASTICO IN TERMINI DI ACCELERAZIONE DI UN ACCELEROGRAMMA O FARE IN AUTOMATICO LA MEDIA DI 5 SPETTRI GENERATI IN CORRISPONDENZA DA ALTRETTANTI ACCELEROGRAMMI.
PER RICHIEDERE L'INTERO PROGETTO scrivetemi SPECIFICANDO DI VOLERE IL PROGETTO PER IL CALCOLO DEGLI SPETTRI DI RISPOSTA ELASTICI.
SEGUONO ALCUNE SCHERMATE OTTENUTE DIRETTAMENTE DALLA ROUTINE SCRITTA IN MATLAB:
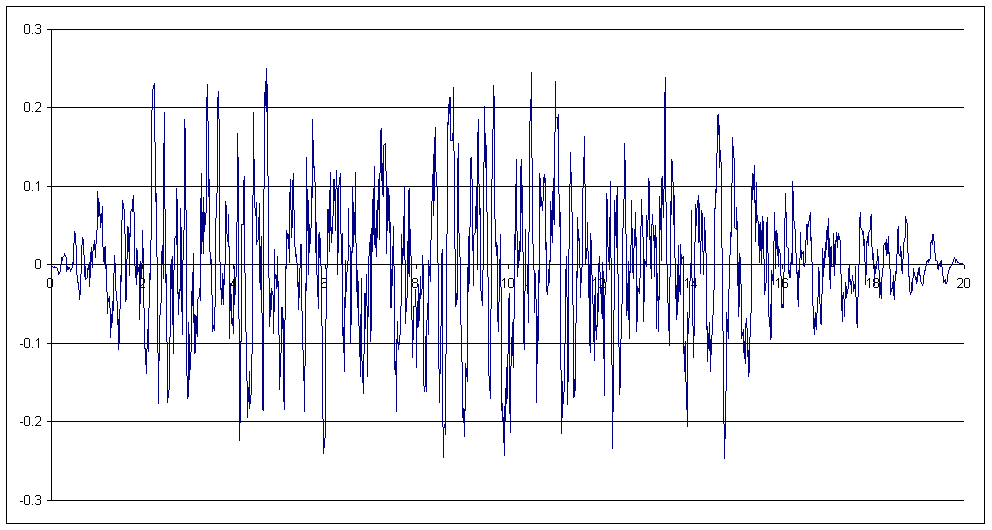
STORIA DELLE ACCELERAZIONI OTTENUTE ARTIFICIALMENTE: ACCELEROGRAMMA SPETTROCOMPATIBILE ARTIFICIALE, GENERATO PARTENDO DALLO SPETTRO ELASTICO DEFINITO DALLA ORDINANZA SISMICA 3274 03/2003 - TERRENO DI CLASSE B